|
|
2020 - 2021 HPS Planning Guide Course I 1st Quarter |
|
1.1
Identifying Integers and Their Opposites |
|
|
|
Time Allocation |
|
|
1 period: 45 min |
|
|
|
|
Content
Standards |
|||||||||||||
|
TEKS |
|||||||||||||
|
Reporting Category: 1.
Numerical Representations and Relationships Knowledge & Skills: 6.2 The
student applies mathematical process standards to represent and use rational
numbers in a variety of forms. |
|||||||||||||
|
Student Expectation: 6.2.B Identify a
number, its opposite, and its absolute value. ELPS: c.1.A use prior knowledge and experiences to understand
meanings in English. |
|||||||||||||
|
Unpacking
Standards |
Examples |
||||||||||||
|
Students
will learn see that the absolute value of a number is its distance from 0. Students use number lines to represent the integers and opposites that are described with language and/or numbers with or without negative symbols. Representation: • Horizontal line • Vertical line |
|
||||||||||||
|
Learning
Target |
|||||||||||||
|
Students will
identify a number and its opposite using a number line. |
|||||||||||||
|
Pre-Requisite Skills: Using number lines (Vertical & horizontal number
lines) |
Understand |
Knowledge |
|||||||||||
|
|
||
|
|
|
|
|
Students understand whole numbers,
fractions, and decimals: • compare and order whole numbers • compare and order fractions • compare and order decimals |
Students recognize, order, and perform
computations with integers: • identify a number and its opposite • compare and order integers using a
number line • find the absolute value of a number |
Students will connect whole numbers
and integers: • locate, compare, and order integers
using a number line • perform operations with integers |
|
|
|
6.1.D: communicate mathematical ideas,
reasoning, and their implications using multiple representations, including
symbols, diagrams, graphs, and language as appropriate. Students
use number lines to represent the integers and opposites that are described
with language and/or numbers with or without negative symbols. In this way,
students are able to make the connections between and become fluent in using
the different representations of integers and their opposites. |
|
|
|
Review
Words: equal greater than less than negative sign number line plus
sign symbol whole number Preview
Words: absolute value inequality integers negative numbers opposites positive
numbers |
|
|
||
|
|
|
|
|
1.1 Identifying
Integers and Their Opposites ● Positive
and Negative Numbers, Explore Activity,
Page 8 ● Opposites,
Explore Activity, Page 8 ● Integers
and Opposites on a Number Line, Lesson,
Page 10 |
||
|
|
|
|
|
Professional Development Video Teacher's Edition (Lesson) (Module) (Unit) Practice and Problem Solving: A/B (PDF) Practice and Problem Solving: C (PDF) |
Example-1 ● Personal Math Trainer - Practice |
|
|
|
|
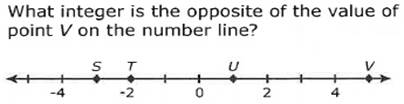
On a number line, opposites are the same distance from 0 but on different
sides of 0. For example, 3 and -3 are opposites. Zero is its own opposite.
For any real number a, its opposite is written -a. The opposite of a number is also called its additive inverse.
This is because the sum of any real number and its opposite is 0. That is,
for any real number a, a + (-a) = 0. This property is known as the Additive
Inverse Property. The opposite of any positive number is negative, and the
opposite of any negative number is positive. The sum of a number and its
opposite is zero, which is neither positive nor negative. An integer’s distance from zero is said to be
non-negative instead of positive. When a distance measurement includes a
negative symbol, the symbol describes the direction rather than the distance. |
|
· TEK 6.2(B) is to include
“identify a number,” however this is NOT included in Go Math o Teacher needs to include
these concepts when teaching this lesson o Vocabulary words
representing “positive” and “negative” need to be covered and reinforced o Be sure to also include
vertical number lines |
|
|
|
|
|
● How
do you identify an integer and its opposite? Look for numbers that are the same distance from zero and on
opposite sides of zero on the number line; for example, -4 and 4. ● How
do you find the opposite of an integer? The opposite of an
integer is the integer the same distance from zero on the other side of 0. If
the integer is 5, then the opposite is -5. If the integer is -3, then the
opposite is 3. |
|
|
|
Day 1 |
|
DIAGNOSTIC ASSESSMENT: Have students complete the diagnostic
assessment (answers)
to determine whether they have the prerequisite skills for Module 1. Use the
assessment to determine if students need intensive or strategic intervention
for the module’s prerequisite skills. Explore Activity-1 (10 minutes): Motivate the Lesson: What
is the coldest weather you have ever experienced? Have you ever experienced a
temperature that is below zero? How do you write a temperature that is below
zero? Begin the Explore Activity to find out. Modeling:
Point out to students that the number line is presented horizontally, but for
elevation it is useful to think of it vertically. You may want to draw a
vertical number line on the board and label the various locations presented
in the table on the vertical number line. Practice &
Homework: Exercises 1 Explore Activity-2 (15 minutes): Connect Vocabulary:
To help students understand the concept of opposite in math and in other
contexts, make a list with students of pairs of opposites, such as hot and
cold, black and white, up and down, left and right. Clarify that left and
right is used in the math concept of opposite with negative numbers to the
left of 0 and positive numbers to the right. Zero is its own opposite. Questioning Strategies: ●
Does every integer have an opposite?
Explain. Yes, zero is its own
opposite. For all other integers, the opposite has a different sign. ●
How does a number line help you
understand what the opposite of an integer is? I can visually see that
4 and -4 are the same distance from zero. Connect to Daily Life:
Explain that bank statements record amounts of money being withdrawn or spent
as negative amounts and amounts of money being deposited as positive amounts.
Check for
Understanding: How do you find the opposite of an
integer? Look for the integer that is the same distance from 0 but on the
other side of zero. Practice &
Homework: Exercises 12, 13, 15, 18, 19, 24 Example-1 (15 minutes): Engage:
Have students take turns graphing an integer and then have another student
graph the integer’s opposite on the number line. Focus on Patterns:
Elicit from students that when finding the opposite of the opposite of a
positive number, the pattern of the signs in the steps is +, -, +. When
finding the opposite of the opposite of a negative number, the pattern of the
signs in the steps is -, +, -. Questioning Strategies: ●
Is the opposite of a temperature
always colder? Explain. No, because if the
temperature is negative, say -5°, then the opposite would be 5°, which would
be warmer. ●
Is the opposite of an opposite always
the number you started with? Give an example. Yes. If you start at 3,
the opposite is -3, then the opposite of -3 is 3. ●
Explain how you could use a number
line to find the opposite of 8. First graph a point 8
units to the right of 0. Then graph a point the same distance to the left of
0. That point will be at -8. Guided Practice: Have
students work on Additional Example 1 and Your Turn, then explain. Your Turn: Avoid Common Error:
If students seem to get lost with the notation “the opposite of the opposite
of,” suggest that they work backward through the sentence. First they find
the opposite of 6, which is -6. Then they find the opposite of -6. Practice & Homework: Exercises 2–10, 14, 16, 17, 20–23 |
|
|
|
Example-1: If students seem to get lost with the
notation “the opposite of the opposite of,” suggest that they work backward through
the sentence. First they find the opposite of 1, which is -1. Then they find
the opposite of -1. Exercise 1:
Remind students to label the points they graph on the number line carefully,
so it is clear which point they intend as the answer. Exercise 9:
Remind students that zero is its own opposite. |
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||
|
●
Assessments ■
Textbook assessment ■
Common assessment ■
Benchmark ■
Released STAAR questions ■
Advanced Placement ●
Lab ●
Project ●
Essay ●
Short answer response |
|
|||||||||||||||||
|
|
|
|
|
Manipulative:
For Explore Activity 2, some
students have difficulty labeling a number line and folding it so the
opposite integers line up. It may be helpful to give them printed number lines
with a vertical dashed line through zero. |
|
|
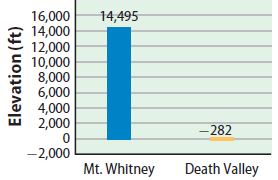
Activity:
If you start at the lowest point, you need to go up 282 ft to
sea level and then another 14,495 ft to get to the top of Mt. Whitney. 282 +
14,495 = 14,777.
|